A utilização dicotômica de “diferença estatisticamente significativa” ou “não significativa” nos ensaios clínicos pode esconder diferenças clinicamente importantes entre os tratamentos. No caso dos ensaios clínicos, o mais importante é se os pesquisadores foram capazes de detectar uma diferença clinicamente significativa entre os tratamentos e qual foi a magnitude dessa diferença. É importante ressaltar que os valores convencionados de significância estatística são guias muito úteis para a interpretação dos resultados, mas não devem ser considerados regras estritas: imaginemos, por exemplo, dois ensaios clínicos, um com um valor de p de 0,05 e outro com um p de 0,06; apesar da diferença mínima, o primeiro seria considerado significativo e o segundo não significativo! Por esse motivo, ao analisarmos um ensaio clínico, devemos olhar além da simples significância estatística.

O Intervalo de confiança

Relatar um intervalo de confiança é um modo alternativo ou complementar muito útil de apresentar os resultados de um ensaio clínico.

Como devemos interpretar o intervalo de confiança? O resultado do ensaio clínico é a melhor estimativa do efeito do tratamento e o intervalo de confiança fornece um intervalo numérico no qual a resposta real da população ao tratamento provavelmente se encontra. Assim sendo, um intervalo de confiança de 95% tem 95% de probabilidade de conter a média real da população. Em outras palavras, o intervalo de confiança fornece uma medida numérica direta da imprecisão da estimativa da resposta ao tratamento, que decorre da variabilidade da amostra.

O que determina a largura do intervalo de confiança? Vários fatores são determinantes, a saber:

• o tamanho da amostra (quanto maior a amostra, menor o intervalo de confiança);

• a variabilidade da resposta que é medida (quanto maior a variabilidade, mais largo é o intervalo);

• o grau de confiança desejado (quanto maior a confiança desejada, mais largo é o intervalo.

Os intervalos de confiança podem ser determinados para médias e suas diferenças, e para proporções e suas diferenças. Isso pode ser feito:

• buscando em tabelas;

• usando fórmulas de cálculo;

• usando programas de computador.

Existe uma estreita relação entre o resultado de um teste de hipótese e o respectivo intervalo de confiança: se a diferença é significativa ao nível de 5%, o intervalo de confiança a nível de 95% exclui a diferença igual a zero.

A vantagem de utilizar intervalos de confiança em vez ou além dos valores de p é que os intervalos de confiança fornecem uma indicação do tamanho das diferenças entre os tratamentos e dão medidas numéricas da inexatidão da nossa estimativa das diferenças reais entre os tratamentos.

Exemplos de interpretação dos intervalos de confiança

Num estudo de psoríase, a diferença na mudança média nos escores PASI de severidade da doença entre os tratamentos com calcipotriol e betametasona foi de 0,18 (5,50 versus 5,32) e o intervalo de confiança a 95% para essa diferença foi -0,40 a 0,78 (Bigby e Gadenne, 1996). Como o intervalo a 95% inclui a diferença zero, nós não podemos estar 95% seguros de que os efeitos da calcipotriol e da betametasona são diferentes.

Os intervalos de confiança podem ser úteis na interpretação de dados de ensaios clínicos nos quais a diferença entre os tratamentos não foi estatisticamente significativa. Nesses casos, devemos olhar para o limite superior do intervalo de confiança a 95%; se esse valor fosse clinicamente importante caso representasse a verdadeira resposta da amostra de pacientes, então um efeito importante de um tratamento pode ter sido perdido nesse estudo!

Intervalo de confiança para a resposta a um único tratamento

Um Intervalo de confiança também pode ser calculado para a proporção de respostas a um único tratamento, utilizando:

• fórmulas;

• tabelas;

• nomogramas;

• programas de computador;

• recursos online.

Usando as mesmas ferramentas acima, também é possível calcular intervalos de confiança para a proporção de efeitos colaterais em um ensaio clínico.

Ensaio clínico sem nenhum efeito adverso

Quando um ensaio clínico não relata a ocorrência de nenhum efeito adverso, também é possível calcular os limites superiores dos intervalos de confiança para a ocorrência “real” de efeitos adversos na população. A regra simples para isso é dividir 3 pelo número de pacientes no estudo (95% de confiança) ou 5 pelo n do estudo (99%) (Rümke, 1975).

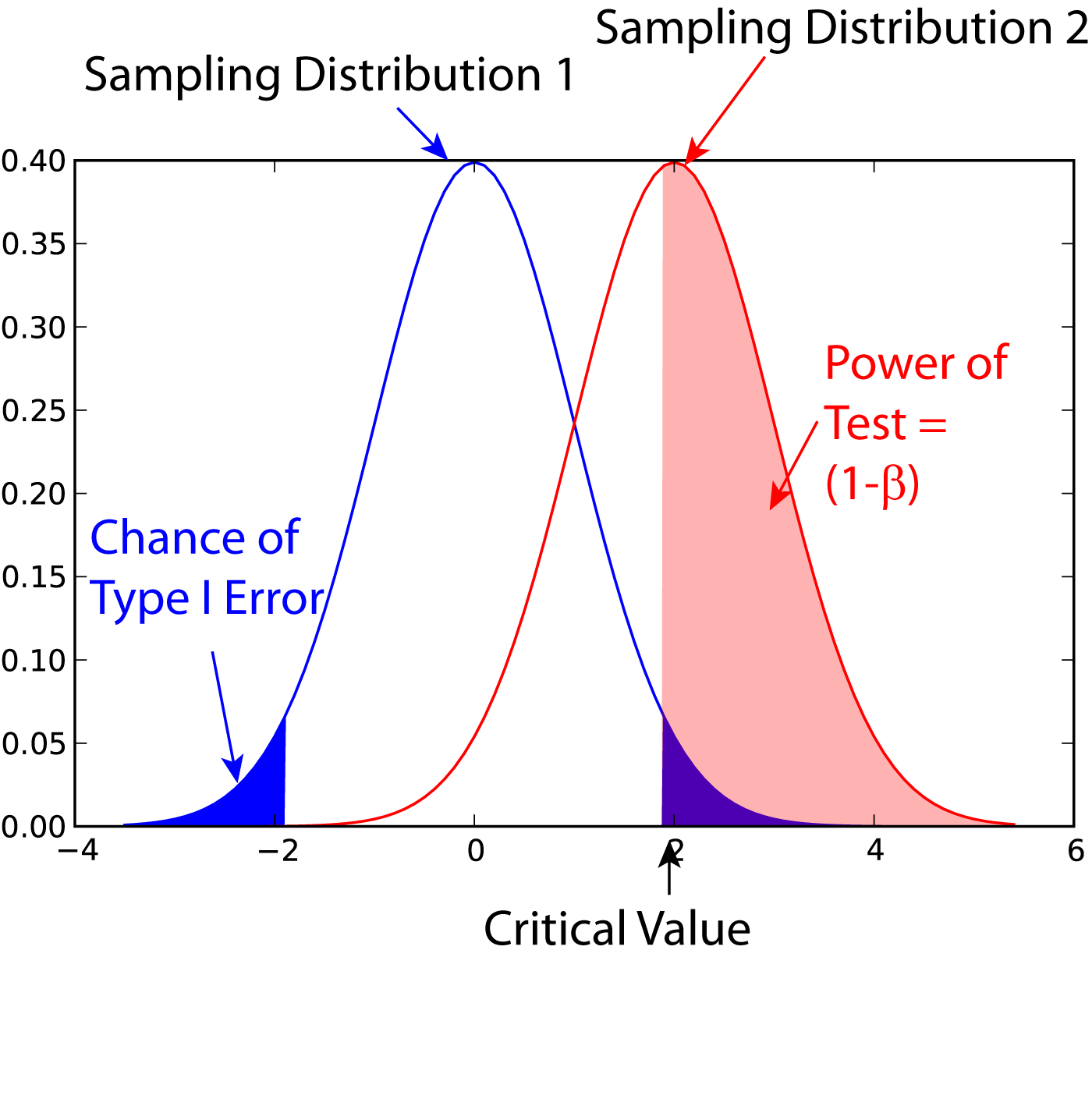
Poder estatístico do ensaio clínico

Muitos efeitos significativos dos tratamentos podem não ser detectados se o número de pacientes estudados for muito pequeno. Consequentemente, muitos estudos com resultados negativos poderiam ter apresentado resultados se o n fosse aumentado!

O poder estatístico (power) é a capacidade de um ensaio clínico de detectar uma diferença entre os tratamentos, caso essa diferença exista.

Num ensaio clínico bem desenhado os pesquisadores deveriam ter uma estimativa das diferenças esperadas entre os tratamentos e conhecimento sobre a magnitude das diferenças que teriam significado clínico. De posse dessas informações, o ensaio clínico deve ser desenhado para incluir um número suficiente de pacientes para assegurar com um grau de certeza razoável que uma diferença estatisticamente significativa será obtida caso existam as diferenças esperadas ou clinicamente significativas. O erro de acreditar que não há diferença entre os tratamentos, quando na realidade estas existem, é um erro tipo 2 ou beta. Os pesquisadores devem decidir que nível de erros tipo beta seria aceitável na pesquisa, e isso determina o poder estatístico buscado para o estudo.

O poder estatístico de um ensaio clínico para detectar uma diferença significativa é determinado pelos seguintes fatores:

• proporção de respostas ao tratamento;

• nível de significância desejado;

• número de pacientes tratados.

O poder estatístico do estudo pode ser calculado utilizando:

• fórmulas;

• nomogramas;

• programas de computador;

• recursos online.

Classicamente, um poder estatístico de 80% com um nível de significância de 0,05 é considerado adequado. Nesse caso, o erro beta é de 0,2. O cálculo do poder estatístico informará o pesquisador sobre o número de pacientes (n) necessário para o ensaio clínico.

Os ensaios clínicos que falham em mostrar uma diferença estatisticamente significativa entre os tratamentos sempre deveriam discutir o poder estatístico do estudo!

Conclusão

A estatística nos ensaios clínicos é uma ferramenta para assegurar que as diferenças observadas entre os tratamentos não se deve apenas ao acaso. Os intervalos de confiança fornecem uma medida da probabilidade de que os resultados de um ensaio clínico sejam devidos ao acaso e da precisão das diferenças estimadas entre os tratamentos.

É bom lembrar que a estatística não informa sobre a significância clínica das diferenças entre os tratamentos. Assim sendo, a falta de diferenças estatisticamente significativas entre os tratamentos não significa que não haja uma diferença clinicamente significativa, pois essa falta de significância pode ser devida ao pequeno tamanho da amostra, com consequente baixo poder estatístico do ensaio clínico.

Referências

Bigby, Michael, and Anne-Sophie Gadenne. 1996. “Understanding and Evaluating Clinical Trials.” Journal of the American Academy of Dermatology 34 (4): 555–90. https://doi.org/10.1016/S0190-9622(96)80053-3.

Rümke, C. L. 1975. “Letter: Implications of the statement: No side effects were observed.” The New England Journal of Medicine 292 (7): 372–73. https://doi.org/10.1056/nejm197502132920723.